Estimación de parámetros
El término estimación de parámetros se
refiere al proceso de utilizar datos de muestra (en ingeniería de
confiabilidad, generalmente datos de tiempos de falla o de éxito) para
estimar los parámetros de la distribución seleccionada. Hay varios
métodos de estimación de parámetros disponibles. Esta sección presenta
una descripción general de los métodos disponibles utilizados en el
análisis de datos de vida. Más específicamente, comenzamos con el método
relativamente simple de trazado de probabilidad y continuamos con los
métodos más sofisticados de regresión de rangos (o mínimos cuadrados),
estimación de máxima verosimilitud y métodos de estimación bayesianos.
Trazado de probabilidad
El
método menos intensivo desde el punto de vista matemático para la
estimación de parámetros es el método de trazado de probabilidades. Como
el término lo implica, el trazado de probabilidad implica un trazado
físico de los datos en
papel de trazado de probabilidad. Este método se implementa fácilmente a mano, dado que se puede obtener el papel trazador de probabilidades adecuado.
El método de trazado de probabilidad toma la CDF (funcion de distribucion acumulativa) de
la distribución e intenta linealizarla empleando un papel especialmente
construido. Las siguientes secciones ilustran los pasos de este método
utilizando la distribución de Weibull de 2 parámetros como ejemplo. Esto
incluye:
- Linealizar la función de falta de fiabilidad
- Construya el papel de trazado de probabilidad
- Determinar las posiciones X e Y de los puntos de la trama
Y luego usar la trama para leer cualquier tiempo particular o valor de confiabilidad/falta de confiabilidad de interés.
Linealización de la función de falta de fiabilidad
En el caso del Weibull de 2 parámetros, la cdf (también la falta de fiabilidad
) está dada por:
-
Esta función puede entonces ser linealizada (es decir, puesta en la forma común de
formato) de la siguiente manera :
-
![{\displaystyle {\begin{aligned}Q(t)=&1-{e^{-\left({\tfrac {t}{\eta }}\right)^{\beta }}}\\\ln( 1-Q(t))=&\ln \left[{e^{-\left({\tfrac {t}{\eta }}\right)^{\beta }}}\right]\\\ln (1-Q(t))=&-\left({\tfrac {t}{\eta }}\right)^{\beta }\\\ln(-\ln(1-Q(t))) =&\beta \left(\ln \left({\frac {t}{\eta }}\right)\right)\\\ln \left(\ln \left({\frac {1}{1- Q(t)}}\right)\right)=&\beta \ln {t}-\beta \ln {\eta }\\\end{aligned}}\,\!}](https://en.wikipedia.org/api/rest_v1/media/math/render/svg/72496b83d8186326dcdbcbe8cc7265d6f69bd6bf)
Luego, configurando:
-
y:
-
la ecuación se puede reescribir como:
-
que ahora es una ecuación lineal con una pendiente de:
-
y un intercepto de:
-
Construyendo el papel
La
siguiente tarea es construir el papel trazador de probabilidad de
Weibull con los ejes y y x apropiados. La transformación del eje x es
simplemente logarítmica. El eje y es un poco más complejo y requiere una
transformación recíproca logarítmica doble, o:
-
dónde es la falta de confiabilidad.
Estos documentos han sido creados por diferentes proveedores y se denominan
Papeles de trazado de probabilidad .
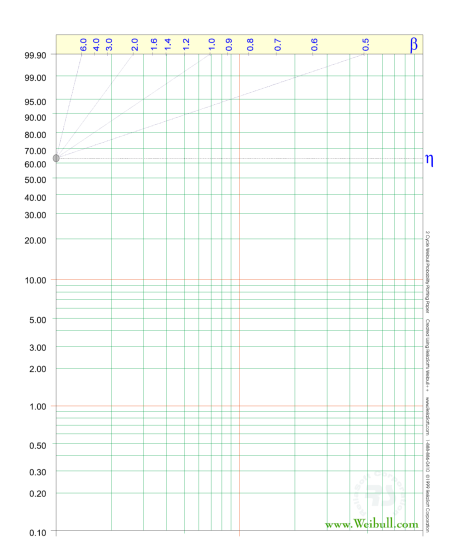
Para ilustrarlo, considere el
siguiente gráfico de probabilidad en un tipo ligeramente diferente de
documento de probabilidad de Weibull.
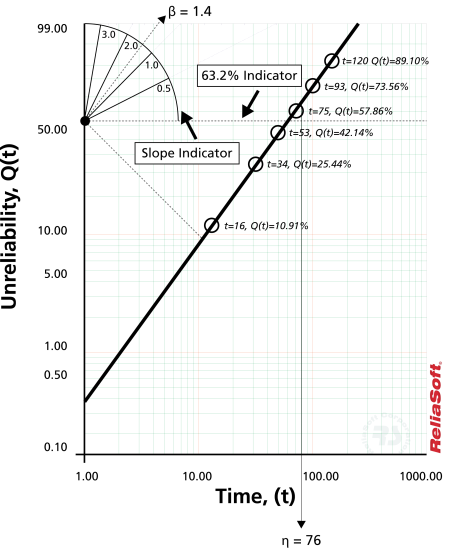
Este artículo está construido
en base a las transformaciones y y x mencionadas, donde el eje y
representa la falta de confiabilidad y el eje x representa el tiempo.
Ambos valores deben conocerse para cada punto de tiempo hasta la falla
que queramos trazar.
Entonces, dada la 
y
valor para cada punto, los puntos se pueden poner fácilmente en la
gráfica. Una vez colocados los puntos en el gráfico, se traza la mejor
línea recta posible a través de estos puntos. Una vez dibujada la línea,
se puede obtener su pendiente (algunos artículos de probabilidad
incluyen un indicador de pendiente para simplificar este cálculo). Este
es el parámetro
, que es el valor de la pendiente. Para determinar el parámetro de escala,
(también llamado el
vida característica ), se lee el tiempo en el eje x correspondiente a
.
Tenga en cuenta que en:
Por lo tanto, si ingresamos el y eje
, el valor correspondiente de
será igual a
. Así, utilizando esta sencilla metodología, se pueden estimar los parámetros de la distribución de Weibull.
Determinación de la posición X e Y de los puntos del gráfico
Los
puntos en el gráfico representan nuestros datos o, más específicamente,
nuestros datos de tiempos de falla. Si, por ejemplo, probáramos cuatro
unidades que fallaron a las 10, 20, 30 y 40 horas, entonces usaríamos
estos tiempos como nuestro
x o valores de tiempo.
Determinar las posiciones apropiadas de y , o los valores de falta de confiabilidad, es un poco más complejo. Para determinar el
Al trazar
posiciones, primero debemos determinar un valor que indique la falta de
confiabilidad correspondiente a esa falla. En otras palabras,
necesitamos obtener el porcentaje acumulado de fallas para cada tiempo
hasta la falla. Por ejemplo, el porcentaje acumulado de fallas a las 10
horas puede ser del 25 %, a las 20 horas del 50 %, y así sucesivamente.
Este es un método simple que ilustra la idea. El problema con este
método simple es el hecho de que el punto del 100% no está definido en
la mayoría de los gráficos de probabilidad; por lo tanto, se debe
utilizar un enfoque alternativo y más sólido. El método más utilizado
para determinar este valor es el método de obtención del
rango medio para cada falla, como se analiza a continuación.
El
método de rangos medianos se utiliza para obtener una estimación de la
falta de confiabilidad de cada falla. El rango mediano es el valor que
tiene la verdadera probabilidad de falla,
, debería tener en el
fracaso de una muestra de
unidades al nivel de confianza del 50%.
La clasificación se puede encontrar para cualquier punto porcentual,
, mayor que cero y menor que uno, resolviendo la ecuación binomial acumulativa para
. Esto representa el rango, o estimación de falta de confiabilidad, para el
fallo en la siguiente ecuación para el binomio acumulativo:
dónde es el tamaño de la muestra y
el número de pedido.
El rango mediano se obtiene resolviendo esta ecuación para
en
:
Por ejemplo, si 
y tenemos cuatro fracasos, resolveríamos la ecuación de rango mediano para el valor de
cuatro veces; una vez por cada falla con
.
Este resultado puede usarse luego como estimación de la falta de
confiabilidad para cada falla o como estimación de la falta de
confiabilidad.
posición de trazado. (Ver también
La distribución de Weibull para ver un ejemplo paso a paso de este método.) La solución de la ecuación binomial acumulativa para
requiere el uso de métodos numéricos.
Enfoque de distribuciones Beta y F
Un
método más directo y sencillo para estimar los rangos medianos es
aplicar dos transformaciones a la ecuación binomial acumulativa, primero
a la distribución beta y luego a la distribución F, lo que da como
resultado
[12, 13] :
dónde 
denota el
distribución en el punto 0,50, con
y
grados de libertad, por falla
fuera de
unidades.
Otra aproximación rápida y menos precisa de los rangos medianos también viene dada por:
Esta aproximación de los rangos medianos también se conoce como aproximación de Benard .
Kaplan-Meier
El estimador de Kaplan-Meier (también conocido como estimador del límite del producto )
se utiliza como alternativa al método de rangos medianos para calcular
las estimaciones de la falta de confiabilidad con fines de trazado de
probabilidad. La ecuación del estimador viene dada por:
dónde:
Ejemplo de trazado de probabilidad
Esta misma metodología se puede aplicar a otras distribuciones con
CDF que
se pueden linealizar. Existen diferentes artículos de probabilidad para
cada distribución, porque diferentes distribuciones tienen diferentes
CDF .
Las herramientas de software de ReliaSoft crean automáticamente estos
gráficos para usted. Las escalas especiales en estos gráficos le
permiten derivar las estimaciones de los parámetros directamente de los
gráficos, de manera similar a la forma
y
se obtuvieron del gráfico de probabilidad de Weibull. El siguiente
ejemplo demuestra el método nuevamente, esta vez usando la distribución
exponencial de 1 parámetro.
Supongamos
que se prueba la confiabilidad de seis unidades idénticas en la misma
aplicación y operación.
niveles de estrés. Todas estas unidades fallan durante la prueba después
de operar durante los siguientes tiempos (en horas): 96, 257, 498, 763,
1051 y 1744.
Los pasos para utilizar el método de trazado de probabilidad para determinar los parámetros del exponencial
pdf que representa el
los datos son los siguientes:
Clasifique los tiempos de falla en orden ascendente como se muestra a continuación.
Obtenga
su rango medio trazando posiciones. Las posiciones de clasificación
media se utilizan en lugar de otros métodos de clasificación porque las
clasificaciones medianas están en un
nivel de confianza específico (50%).
Los tiempos hasta el fracaso, con sus correspondientes rangos medios, se muestran a continuación:
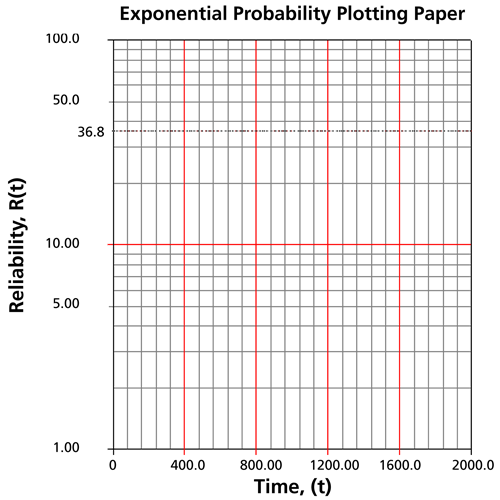
En un papel de probabilidad exponencial, traza los tiempos en el eje x y sus correspondientes
valor de clasificación en el eje y. La siguiente figura muestra un ejemplo de un artículo de probabilidad exponencial. El
El papel es simplemente un papel log-lineal.
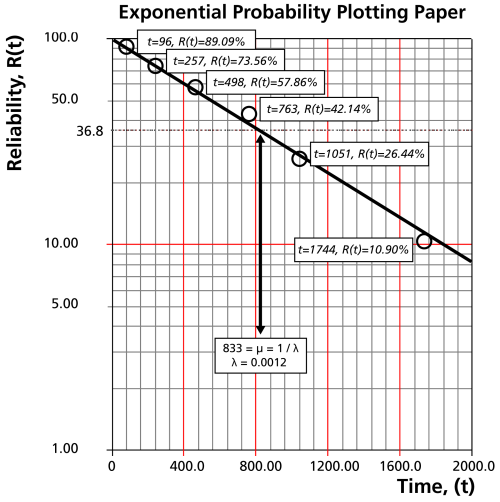
Traza la mejor línea recta posible que pase por el
y
punto y a través de los puntos trazados (como se muestra en el gráfico siguiente).
Al o
punto de ordenadas, dibuja un
línea recta horizontal hasta que esta línea se cruce con la línea recta
ajustada. Dibuja una línea vertical a través de esta intersección hasta
que cruce la abscisa. El valor en la intersección de las abscisas es la
estimación de la media. Para este caso,
horas lo que significa que
(Esto siempre es del 63,2% porque
.
Ahora cualquier valor de confiabilidad para cualquier tiempo de misión.
se puede obtener. Por ejemplo, el
La confiabilidad para una misión de 15 horas, o en cualquier otro
momento, ahora se puede obtener a partir de la trama o analíticamente.
Para obtener el valor del gráfico, dibuje una línea vertical desde la abscisa, en
horas, hasta la línea ajustada. Dibuja una línea horizontal desde esta intersección hasta la ordenada y lee
. En este caso,
. Esto también se puede obtener
analíticamente, a partir de la función de confiabilidad exponencial.
Además
del inconveniente más obvio del trazado de probabilidades, que es la
cantidad de esfuerzo requerido, el trazado de probabilidades manual no
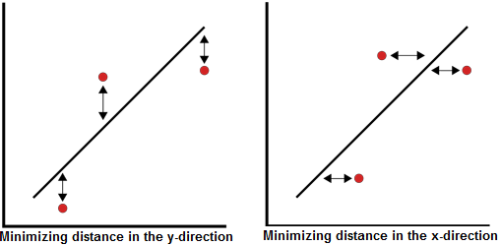
siempre es consistente en los resultados. Dos personas que trazan una
línea recta a través de un conjunto de puntos no siempre trazarán esta
línea de la misma manera y, por lo tanto, obtendrán resultados
ligeramente diferentes. Este método se utilizó principalmente antes del
uso generalizado de computadoras que podían realizar fácilmente los
cálculos para métodos de estimación de parámetros más complicados, como
los métodos de mínimos cuadrados y máxima verosimilitud.
